
"Matemática, a diversão dos gênios."
"Como dizem os sábios sem a matemática, os gênios não sobrevivem." Porque não construir o mundo da matemática numa verdadeira diversão.Sem esse enigma:"matemática como é dificil!". Talvez nestas palavras resume como é "difícil" lhe dar com a matemática nas escolas,em casa, no trabalho, enfim,no próprio preceito dessa matéria. Sendo assim, convido a todos a discutir, ensinar, aprender, compartilhar algo novo. " SOMOS TODOS ANJOS DE UMA ASA SÓ. SÓ VOAMOS SE NOS ABRAÇARMOS." (M.Gandhi)
terça-feira, 18 de maio de 2010
 ções do Teorema de Pitágoras
ções do Teorema de PitágorasTeorema de Pitágoras é uma importante ferramenta utilizada na Matemática, principalmente na área da Geometria. Esse teorema é atribuído ao filósofo grego Pitágoras de Samos, fundador da ilustre escola pitagórica,
O Teorema de Pitágoras é atribuído ao triângulo retângulo, onde ele relaciona os catetos e a hipotenusa através da seguinte lei de formação:
“a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.”
Obs: a = cateto 1, b = cateto 2, c = hipotenusa

Exemplo 1
Uma escada apoiada em uma parede tem sua base distante cerca de 6 metros da parede. Sabendo que a parede mede cerca de 8 metros, determine o comprimento da escada.

x² = 8² + 6²
x² = 64 + 36
x² = 100
x = √100
x = 10
A escada possui 10 metros de comprimento.
Exemplo 2
A diagonal divide o retângulo em dois triângulos retângulos, consistindo na hipotenusa deles.
Portanto, utilizaremos o Teorema de Pitágoras para determinar a medida da diagonal. Veja:
d² = 30² + 20²
quarta-feira, 12 de maio de 2010
“ Sem conhecer a Geometria a leitura interpretativa do mundo torna-se incompleta, a comunicação das idéias fica reduzida e a visão da Matemática torna-se distorcida. ”(LORENZATO, 1995, p.5)
Muitos autores se referem à importância do estudo da geometria, não apenas por suas possibilidades de organização e representação do espaço em que vivemos, mas também pelos aportes que os recursos geométricos oferecem à resolução de Problemas da vida cotidiana, ao desempenho de determinadas atividades profissionais ou à própria compreensão de outros conteúdos escolares. (FONSECA et al., 2001, p.92)
Tendências para o Ensino de Geometrias para 5ª a 8ª séries
•Apresentação da geometria como meio de descrever o mundo físico.
•Explorar as transformações de figuras geométricas através de rotação, translação, simetria e deformação, ressaltando a semelhança e a congruência.
•Utilizar a Geometria como auxiliar para resolver problemas. •Aplicar propriedades geométricas.
•Favorecer a emissão e a verificação de hipóteses.
•Integrar a Geometria com a Aritmética e Álgebra.
Os estudos de Geometria da 5ª à 8ª série devem favorecer as oportunidades para os alunos realizarem suas primeiras explorações de modo sistemático. É nessa fase que as primeiras deduções lógicas são construídas; os resultados e os processos devem ser discutidos, embora sem a preocupação com sua formalização. O vocabulário próprio da Geometria também deve ser empregado corretamente, com vistas ao domínio das definições e das propriedades. A exploração informal da Geometria é muito adequada e necessária. Devem ser oferecidas oportunidades de comparação, classificação, medição, representação, construção, transformação,...
O Campo de Futebol
Se observamos o campo de futebol podemos identificar nele várias figuras geométricas, vários ângulos, segmentos de retas, pontos, circunferências, raio, diâmetro, perímetro, áreas, diagonais, arco, podemos trabalhar com medidas e suas transformações, ou seja, metros e centímetros.
Você já calculou o perímetro de um campo de futebol, suas áreas, área do gol, a área do círculo central, seu diâmetro, a diagonal do campo, são alguns tópicos que iremos mostrar baseado na figura 21 e 22:
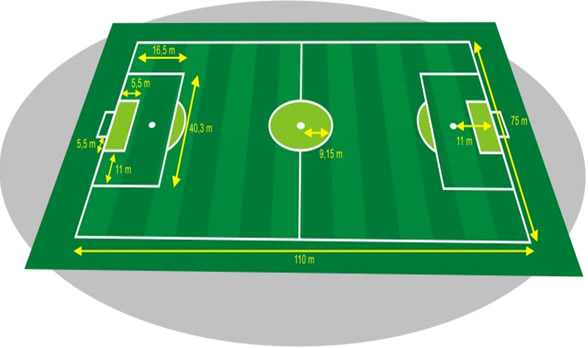
Figura 21: O campo e suas medidas oficiais
Um campo de futebol tem 110 m de comprimento e 75 m de largura, qual o seu perímetro, ou seja, a medida do contorno do campo?
Perímetro = 2 x ( b + h ) , onde, b = comprimento e h = largura
P = 110 m + 110 m + 75 m + 75 m = 2 x ( 110 m + 75 m )
P = 2 x ( 185 m )
P = 370 m
O perímetro é de 370 m.
Já sabemos que as dimensões do campo de futebol são 110 m x 75 m, vamos calcular agora sua área:
Área = Base x Altura ( A = b.h ), onde, b = comprimento e h = largura
Medidas do campo = 110 m x 75 m
Ado campo = 110 m x 75 m
Ado campo = 8.250 m²
O campo de futebol possui 8.250 m².
Sabendo que a área total do campo é 8.250 m², e nessa área estão 22 jogadores, vamos calcular a área equivalente a cada um desses 22 jogadores.
Campo = 8.250 m²
Números de jogadores = 22
Ade cada jogador = 8.250 m² / 22 (área total de 8.250 m² dividida por 22 jogadores)
Ade cada jogador = 375 m²
Cada jogador pode ocupar uma área de 375 m².
Agora iremos calcular a área que o goleiro tem que defender e o atacante tem para acertar e fazer o gol. As medidas das traves são 7,32 m de largura e 2,44 m de altura, conhecendo essas medidas podemos calcular a área que o goleiro tem que defender.
Área = b x h, onde, b = comprimento e h = largura
Ado gol = 7,32 m x 2,44 m
Ado gol = 17,86 m²
A área entre as traves é de 17,86 m², ou seja, o goleiro tem que defender uma área mais de 17 metros quadrados.
Como estamos calculando várias áreas, podemos calcular também a área da grande área onde o goleiro pode trabalhar com a mão. A grande área tem 16,5 m de comprimento e 40,3 m de largura, com esses dados podemos calcular a área que o goleiro tem para trabalhar com as mãos.
Ada grande área = b x h, onde, b = comprimento e h = largura
Ada grande área = 16,5 m x 40,3m
Ada grande área = 664,95 m²
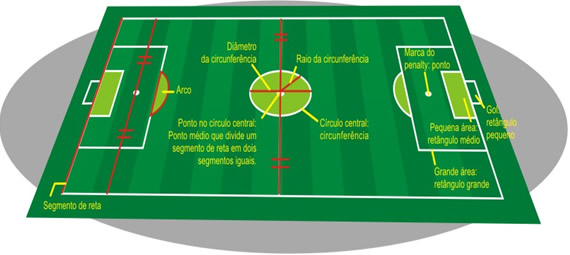
Figura 22: Futebol e a geometria
Agora iremos calcular a área do círculo central. O diâmetro do círculo central é de 18,30 m, atribuindo a ? ( pi ) o valor de 3,14 calcule a área do círculo central:
Área do círculo central = ? x r², onde, ? = pi = 3,14 e r = raioDiâmetro = 18,30 m e ? = 3,14
r = Diâmetro / 2 ? r = 18,30 / 2 ? r = 9,15 m
Ado círculo central = 3,14 x ( 9,15 m )²
Ado círculo central = 3,14 x 83,72 m²
Ado círculo central = 262,88 m²
O círculo central possui então uma área de 262,88 m².
Testando o Raciocínio
QUANTOS SÃO?
Quantos quadrados você vê na figura abaixo? E quantos retângulos?

postado por Márcio Dênis, no dia 12 de maio de 2010.
terça-feira, 11 de maio de 2010
Poliedros
Afirmar que poliedro são sólidos formados por faces (partes limitadas de um plano), pode dar uma ideia do que eles sejam, mas não serve absolutamente como definição; aliás, uma das grandes dificuldades para o desenvolvimento desse tema, bem como fazer demonstrações dos teoremas sobre poliedros, estava justamente na falta de uma definição precisa do significado dessa palavra.
Definição
seguinte definição nos dá uma idéia do que é poliedro, então definiremos assim:
“Poliedro é uma reunião de um número finito de polígonos planos, onde cada lado de um desses polígonos é também lado de um, e apenas um, outro polígono”
Vejam os seguintes exemplos:

OBS: Podemos também encontrar como definição para poliedros, o seguinte: É um sólido limitado por polígonos, que tem, dois a dois, um lado comum.
Cada poliedro é formado pela reunião de um número finito de regiões poligonais planas, chamadas de faces. Cada lado de uma região poligonal, comum a exatamente duas faces, é chamada aresta do poliedro. E cada vértice de uma face é um vértice do poliedro. Veja:

Poliedro convexo e Poliedro não-convexo
observe as figuras abaixo:

Qual dessas figuras você classificaria como poliedro convexo e como poliedro não convexo?
A resposta para essa indagação fica mais fácil quando temos conhecimento de que:
“Um poliedro é convexo se qualquer reta (não paralela a nenhuma de suas faces) o corta em, no máximo, dois pontos”.
Logo, podemos concluir, que o poliedro convexo está representado pela figura 02, e a figura 03 é um exemplo de poliedro não-convexo.
Teorema de Euler
O matemático suíço Leonhard Euler (1707 – 1783) descobriu uma importante relação entre o número de vértice (V), o número de aresta (A) e o número de faces (F) de um poliedro convexo.
O teorema de Euler foi descoberto em 1758. Desde então diversas demonstrações apareceram na literatura e algumas continham falhas (como a de Cauchy), que foram descobertas muitos anos mais tarde. Essas falhas eram devidas à falta de precisão na definição de poliedro. Mesmo Euler nunca se preocupou em definir precisamente essa palavra.
Em todo poliedro com A arestas, V vértices e F faces, vale a relação:
V – A + F = 2
Exercícios Resolvidos
1º) Arquimedes descobriu um poliedro convexo formado por 12 faces pentagonais e 20 faces hexagonais, todas regulares. Esse poliedro inspirou a fabricação da bola de futebol que apareceu pela primeira vez na Copa do Mundo de 1970. Quantos vértices possui esse poliedro?

Resolução:
Como o poliedro tem 12 faces pentagonais, então:
12 . 5 = 60
O poliedro tem 20 faces hexagonais, assim 20 . 6 = 120, logo:
F = 12 + 20 = 32
Cada aresta foi contada duas vezes, portanto temos:
2A = 60 + 120
2A = 180
A = 180/2
A = 90
Como o poliedro é convexo, vale a relação de Euler,
V – A + F = 2, portanto:
V – 90 + 32 = 2
V = 2 + 90 – 32
V = 92 - 32
V = 60
Assim, o número de vértices é 60.
2º) Determinar o número de arestas e o número de vértices de um poliedro convexo com 6 faces quadrangulares e 4 faces triangulares.
Resolução:
Como o poliedro tem 6 faces quadrangulares, calculamos: 6 . 4 = 24
O poliedro tem 4 faces triangulares: 4 . 3 = 12
Como cada aresta foi contada duas vezes, o número total de arestas é:
A = (24+12)/2 = 18
Temos então F = 10, A = 18. Aplicando a relação de Euler:
V – A + F = 2
V – 18 + 10 = 2
V = 18 - 10 + 2
V = 8 + 2
V = 10
Logo, o poliedro tem 18 arestas e 10 vértices.
Exercícios para praticar
1º) Determine o número de vértices de um poliedro convexo que tem três faces triangulares, uma face quadrangular, uma face pentagonal e duas faces hexagonais.
2º) (PUC –SP) O número de vértices de um poliedro convexo que possui 12 faces triangulares é:
a) 4 b) 12 c) 10 d) 6 e) 8
postado Márcio Dênis , 11 de maio de 2010.
Referências Bibliográficas: DANTE,Luiz Roberto. Matemática, volume único. São Paulo: Editora Ática, 2005.Lima, Elon Lages; Carvalho, Paulo Cezar Pinto; Wagner Eduardo; Morgado Augusto Cesar. Matemática do Ensino Médio, Volume 2.Rio de Janeiro: Editora Sociedade Brasileira de Matemática.
segunda-feira, 10 de maio de 2010
Geometria Plana e Espacial
Elementos de Geometria plana
Geometria Plana do ponto de vista elementar. As principais figuras planas são apresentadas e existe um forte apelo visual.
Um triângulo equilátero
Triângulo difícil. Deve-se realizar várias operações algébricas envolvendo equações do segundo grau. Apresentamos outra forma para obter a área de um triângulo. Apresentamos um problema simples que costuma deixar muita gente "quebrando a cabeça".
Um triângulo isósceles
Triângulo especial que tem aparecido em alguns vestibulares. Para obter o ângulo procurado deve-se realizar muitas operações algébricas e tem-se a impressão de estarmos calculando o ângulo de uma forma cíclica sem a possibilidade de obter a resposta desejada. A solução faz uso forte da lei dos senos para um triângulo.
Círculo, circunferência e arcos
Aplicações da circunferência. Circunferência. Círculo. Pontos interiores e exteriores a uma circunferência. Raio, corda e diâmetro. Posições relativas de: retas e circunferência, de secantes e tangentes a uma circunferência, de duas circunferências, de segmentos tangentes a circunferências. Polígonos inscritos e circunscritos na circunferência. Arco de circunferência e ângulo central. Propriedades de arcos e cordas. Ângulo inscrito, semi-inscrito e arco capaz. Outras propriedades com cordas e segmentos.
Áreas de regiões poligonais
O Triângulo e uma região triangular. O conceito de região poligonal. Unidade de área. Cálculo da área do: retângulo, quadrado, paralelogramo, triângulo, losango, trapézio. Áreas de triângulos semelhantes. Polígonos regulares e seus elementos. Áreas de polígonos regulares. Áreas de polígonos semelhantes.
Áreas de regiões circulares
O círculo como limite de regiões poligonais regulares. Perímetro e Área do Círculo. Arcos. Setor circular. Segmento circular. Curiosidades sobre o número Pi.
Exercícios de áreas de regiões poligonais
Exercícios Resolvidos sobre Áreas de regiões poligonais.
Exercícios de áreas de regiões circulares
Exercícios Resolvidos sobre Áreas de regiões circulares.
Geometria analítica plana
Geometria Analítica plana, iniciando com as coordenadas no plano e dando ênfase no estudo das equações da reta. Também são estudadas as curvas cônicas nas suas formas padrões.
Fórmula de Heron: área de região triangular
Demonstração da Fórmula de Heron. Exercício resolvido. Programa on-line para calcular áreas de regiões triangulares, conhecidos os três lados.
Vetores no plano cartesiano
Vetores no plano Euclidiano e suas propriedades. O Plano cartesiano como um Espaço Vetorial bidimensional. Interpretação geométrica do produto escalar e suas principais propriedades.
Geometria Espacial
Elementos de Geometria Espacial
Elementos gerais sobre a Geometria Espacial. Veja nossos outros links sobre Geometria espacial.
A noção de espaço
Um conceito de espaço. O que é um Sistema de Coordenadas e como este conceito aparece em nosso cotidiano. Outros sistemas de Coordenadas, como: coordenadas polares, cilíndricas, esféricas e um sistema geográfico de coordenadas. Uma idéia do que é o espaço R4. Exemplo de como o ser humano pode ser pensado como um objeto em R5. Algumas idéias sobre a inflação e uma análise deste objeto tão maltratado à luz da noção de Espaço. Exercícios.
Cilindros
O cilindro e o seu uso no nosso cotidiano. Exemplos onde este conceito é utilizado. Cilindros são superfícies e não sólidos como encontramos em muitos livros. Estendemos o conceito de cilindro a algo não usual. Lista de elementos geométricos do cilindro. Cálculo das áreas lateral e total do cilindro, assim como o volume da região envolvida pela superfície cilíndrica.
Cones
Cone e seus elementos: base, vértice, eixo, altura, geratriz, superfície lateral, superfície do cone, seção meridiana. Cones: circular, elíptico, reto e oblíquo. Áreas lateral e total do cone. Cone equilátero. Exercícios resolvidos.
Esferas
Aplicações da esfera. Aplicação prática da esfera no cálculo de volumes de recipientes onde se conhece a altura do líquido. A esfera é apresentada como uma superfície, ao contrário de algumas outras que sugerem que a esfera seja um sólido. Fórmulas não triviais para obter cálculos de áreas e volumes de objetos esféricos. Cálculo do volume de calotas nos hemisférios Sul e Norte. Demonstração de uma fórmula não trivial com o uso do Cálculo Diferencial e Integral. Programa escrito em Javascript para a realização de Cálculos On Line de elementos esféricos.
Pirâmides
Pirâmides: Elementos e Classificação. Pirâmide regular reta. Área lateral de uma pirâmide. Área total de uma pirâmide. Volume de uma pirâmide. Seção transversal de uma pirâmide.
Poliedros
Poliedros e os seus elementos: Faces, Arestas e Vértices. Poliedros convexos e as relações de Euler. Poliedros regulares e importantes relações matemáticas relacionadas com eles. Tabelas com elementos para o cálculo do raio do círculo inscrito, raio do círculo circunscrito, ângulo diedral, área lateral e volume de um poliedro regular convexo.
Prismas
Prisma e os seus tipos principais, de acordo com a inclinação das arestas laterais. As seções transversal e reta de um prisma. A planificação do prisma. Cálculos das áreas lateral e total do prisma e do volume do mesmo. O tronco de um prisma e o seu volume.
Vetores no espaço R³
Conexão entre vetores de R2 e R3. Os conceitos de: Vetor em R3, soma de vetores e suas propriedades, aplicações geométricas, produto de escalar por vetor e suas principais propriedades, módulo de um vetor, vetores unitários e a importância desse conceito. Produto escalar e as suas propriedades. O ângulo entre dois vetores com o produto escalar. Vetores ortogonais, produto vetorial e suas propriedades. O ângulo entre dois vetores com o produto vetorial. O produto vetorial ao cálculo de áreas de paralelogramos e triângulos. Produto misto e o seu uso no cálculo de volumes de paralelepípedos e tetraedros não regulares.
Construída por Ulysses Sodré.
Atualizada em 24/mar/2005.